Publications

2026

1. bioRxiv 2026

   Generating and navigating single cell dynamics via a geodesic bridge between nonlinear transcriptional and linear latent manifolds

   Junchao Zhu^†, Zhenyi Zhang^†, Yuhao Sun^†, Hao Dai, Han Wen, Peijie Zhou^*, and Luonan Chen^*

   bioRxiv, Apr 2026

   Abs DOI HTML

   Time-series single-cell RNA sequencing (scRNA-seq) captures cellular processes as sparse and unpaired snapshots, limiting our ability not only to reconstruct continuous cell state transitions, but also to navigate between states in a controlled and interpretable manner. Here we present GeoBridge, a framework modeling cellular dynamics as geodesic trajectories on the transcriptional manifold based on isometric geodesic theory. By learning the geodesic bridge mapping, the method theoretically and computationally transforms time-varying nonlinear transcriptional geodesics (original nonlinear manifold) into constant-velocity straight-line geodesics (latent linear manifold). In the learned geodesic space, continuous interpolation becomes biologically meaningful, enabling reconstruction of unobserved intermediate states and efficient navigation between distinct cellular phenotypes at a single-cell resolution. By mapping interpolated trajectories back to the original gene expression space, GeoBridge recovers smooth transcriptional programs that are robust to noise and snapshot sparsity. Leveraging the derived geodesic potentials, GeoBridge further infers pseudo-temporal trajectories with superior fidelity compared to mainstream approaches from single-snapshot scRNA-seq data without temporal annotation, and directly identifies genes that drive progression along transition paths. We demonstrate the utility of GeoBridge across diverse systems, where GeoBridge resolves EMT-MET progression in cancer stem cells and identifies stage-specific modules as well as the branching cell-fate dynamics in human pluripotent stem cells with higher reconstruction accuracy than state-of-art methods. More importantly, GeoBridge supports single-cell fate navigation in multi-target hematopoietic lineages, allowing neutrophil-biased cells to be virtually guided toward mast-cell fates along biologically plausible paths. Together, GeoBridge establishes a principled method that transforms sparse single-cell measurements into a continuous, controllable landscape for the reconstruction, navigation and manipulation of cellular state transitions.

2. bioRxiv 2026

   Benchmarking zero-shot single-cell foundation model embeddings for cellular dynamics reconstruction

   Xueya Zhou, Zihan Wang, Yue Ling, Qinxue Tian, Zhenyi Zhang, Yongge Li, Luonan Chen^*, and Peijie Zhou^*

   bioRxiv, Mar 2026

   Abs DOI HTML

   Reconstructing cellular trajectories from time-resolved single-cell transcriptomics is fundamental to understanding processes from embryonic development to cancer progression. While single-cell foundation models (scFMs) promise universal biological representations through large-scale pretraining, their capacity to capture the non-linear dynamics governing cell-fate decisions remains uncharacterized. Here we systematically benchmark multiple scFMs across challenging biomedical scenarios involving branching lineages and continuous state transitions. By coupling zero-shot scFM embeddings with dynamic optimal transport, we evaluated their performance against a traditional highly variable gene (HVG) baseline in backtracking progenitor states, interpolating transition intermediates, and extrapolating future fates. We find that zero-shot scFM embeddings underperform the HVG baseline across diverse biological systems, particularly in recovering the distributional complexity of unobserved cells. Mechanistic analysis reveals that current scFM architectures tend to over-compress subtle temporal signals, causing an artificial "linearization" of branched biological structures that may obscure critical divergence points in disease progression. Our findings suggest that while scFMs provide unified cell-state views, the HVG baseline remains more robust for trajectory inference, identifying a fundamental "temporal-compression" bottleneck that must be addressed to develop next-generation, dynamics-aware foundation models.

3. SSRN 2026

   NICE: A Two-Step Non-Invasive Framework for Embryo cfDNA Read Enrichment and Quality Assessment

   Xueya Zhou, Shu Ding, Zhenyi Zhang, Qiaoling Shangguan, Jie Qiao^*, Peijie Zhou^*, and Yidong Chen^*

   SSRN, Mar 2026

   DOI HTML

2025

1. ICLR 2025 oral

   

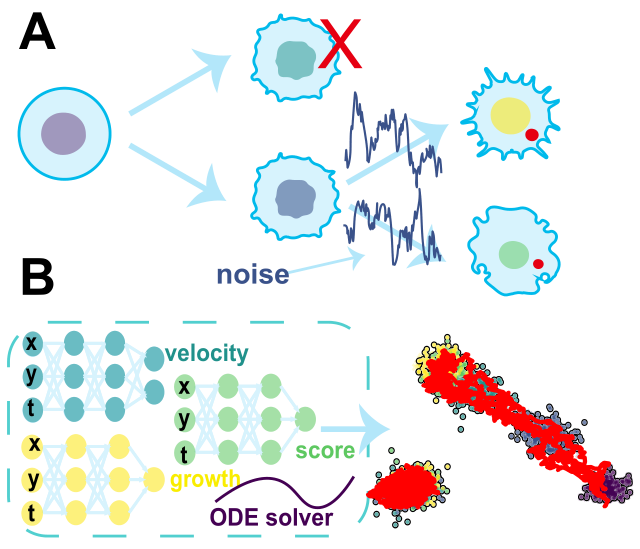   Learning stochastic dynamics from snapshots through regularized unbalanced optimal transport

   Zhenyi Zhang^†, Tiejun Li^*, and Peijie Zhou^*

   International Conference on Learning Representations  (ICLR Oral,  1.8%) , Mar 2025

   Abs DOI HTML

   Reconstructing dynamics using samples from sparsely time-resolved snapshots is an important problem in both natural sciences and machine learning. Here, we introduce a new deep learning approach for solving regularized unbalanced optimal transport (RUOT) and inferring continuous unbalanced stochastic dynamics from observed snapshots. Based on the RUOT form, our method models these dynamics without requiring prior knowledge of growth and death processes or additional information, allowing them to be learnt directly from data. Theoretically, we explore the connections between the RUOT and Schrödinger bridge problem and discuss the key challenges and potential solutions. The effectiveness of our method is demonstrated with a synthetic gene regulatory network. Compared with other methods, our approach accurately identifies growth and transition patterns, eliminates false transitions, and constructs the Waddington developmental landscape.

2. NeurIPS 2025

   

   Modeling Cell Dynamics and Interactions with Unbalanced Mean Field Schrödinger Bridge

   Zhenyi Zhang^†, Zihan Wang^†, Yuhao Sun^†, Tiejun Li^*, and Peijie Zhou^*

   Advances in Neural Information Processing Systems  (NeurIPS) , May 2025

   Abs DOI HTML

   Modeling the dynamics from sparsely time-resolved snapshot data is crucial for understanding complex cellular processes and behavior. Existing methods leverage optimal transport, Schrödinger bridge theory, or their variants to simultaneously infer stochastic, unbalanced dynamics from snapshot data. However, these approaches remain limited in their ability to account for cell-cell interactions. This integration is essential in real-world scenarios since intercellular communications are fundamental life processes and can influence cell state-transition dynamics. To address this challenge, we formulate the Unbalanced Mean-Field Schrödinger Bridge (UMFSB) framework to model unbalanced stochastic interaction dynamics from snapshot data. Inspired by this framework, we further propose CytoBridge, a deep learning algorithm designed to approximate the UMFSB problem. By explicitly modeling cellular transitions, proliferation, and interactions through neural networks, CytoBridge offers the flexibility to learn these processes directly from data. The effectiveness of our method has been extensively validated using both synthetic gene regulatory data and real scRNA-seq datasets. Compared to existing methods, CytoBridge identifies growth, transition, and interaction patterns, eliminates false transitions, and reconstructs the developmental landscape with greater accuracy.

3. npj Syst. Biol. Appl.

   

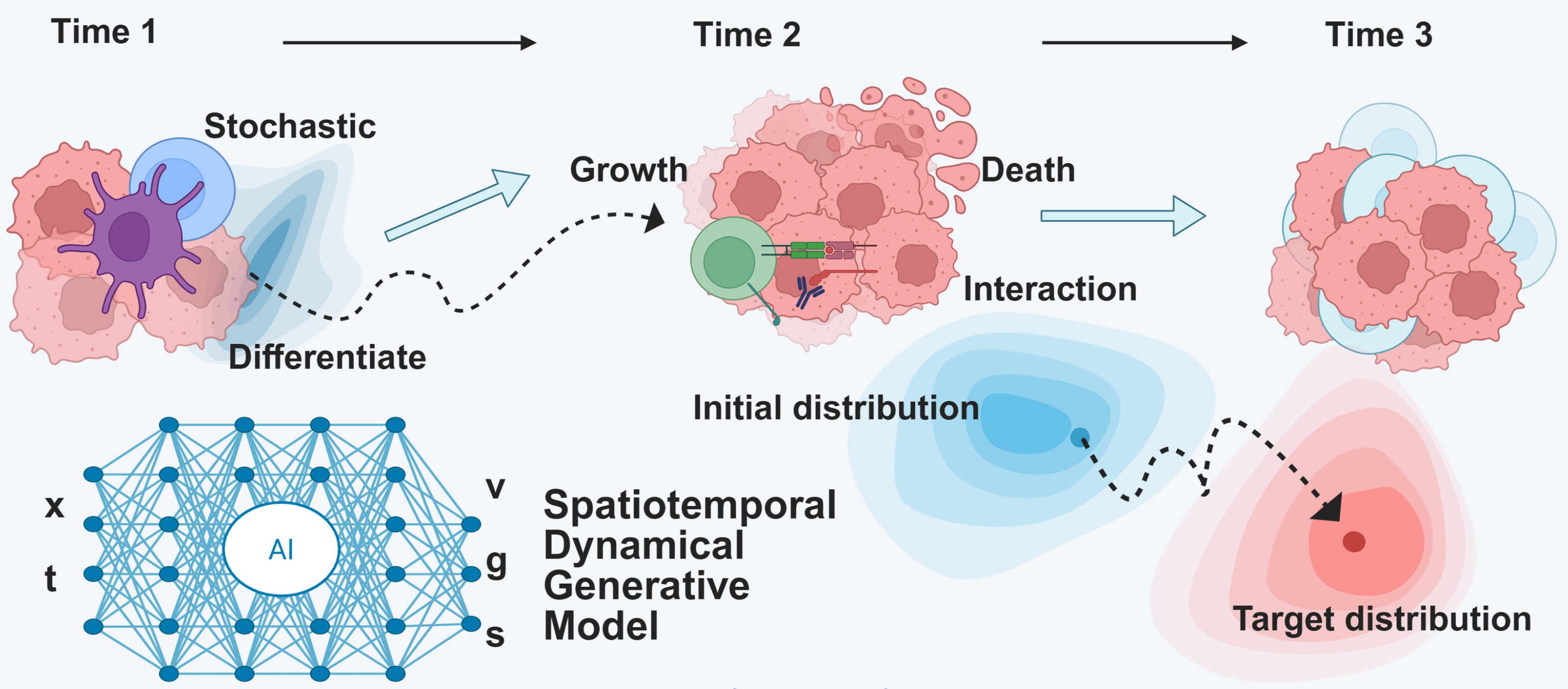   Deciphering cell-fate trajectories using spatiotemporal single-cell transcriptomic data

   Zhenyi Zhang^†, Zihan Wang^†, Yuhao Sun^†, Jiantao Shen^†, Qiangwei Peng^†, Tiejun Li^*, and Peijie Zhou^*

   npj Systems Biology and Applications, Sep 2025

   Abs DOI HTML

   Cellular processes evolve dynamically across time and space. Single-cell and spatial omics technologies have provided high-resolution snapshots of gene expression, greatly expanding the capability to characterize cellular states. This review summarizes recent modeling strategies for time-series and spatiotemporal transcriptomic data, emphasizing links between dynamical systems, generative modeling, and biological insight. These approaches illustrate how computational tools can deepen our understanding of the dynamic nature of single cells.

4. Adv. Sci.

   

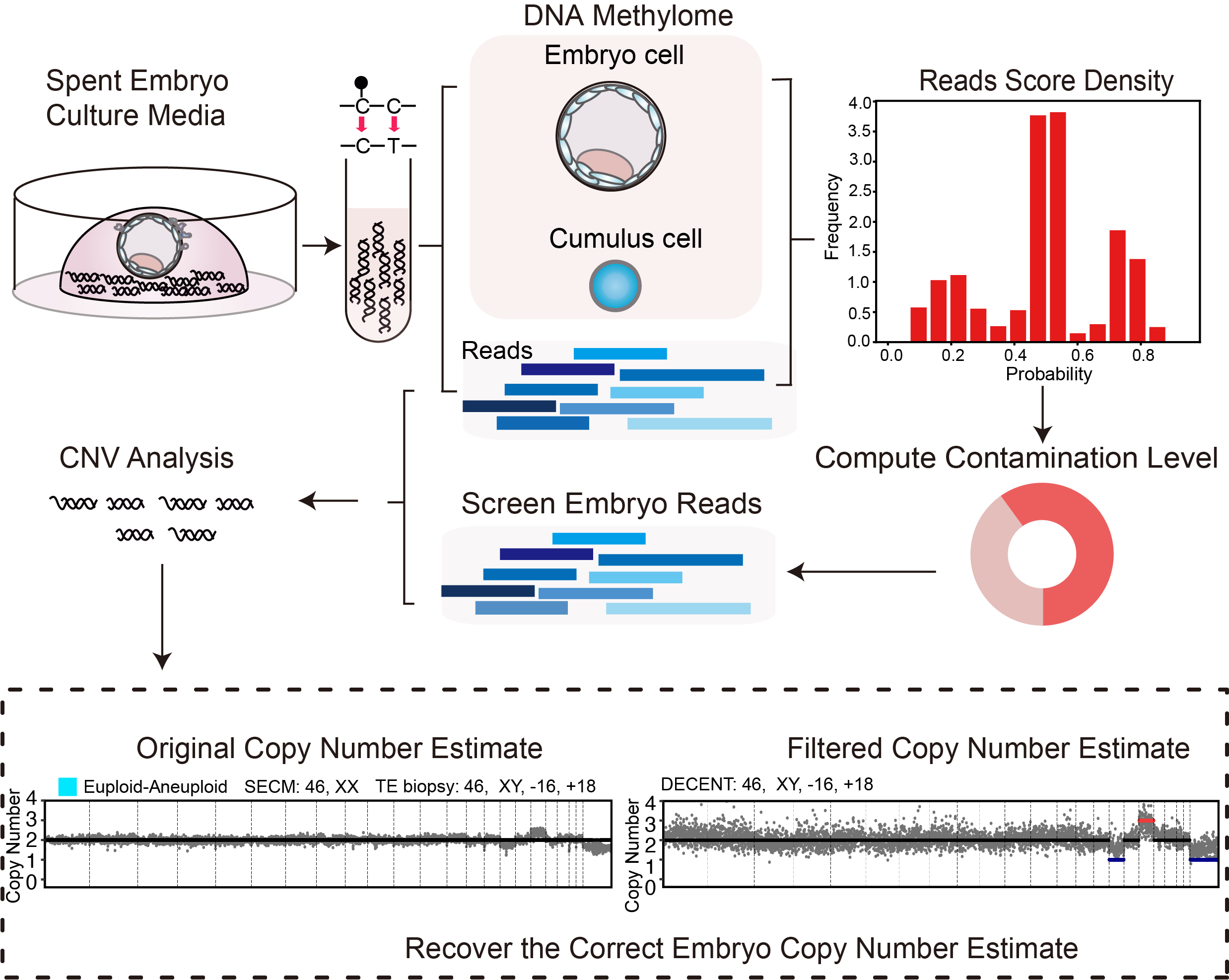   Genetic deconvolution of embryonic and maternal cell-free DNA in spent culture medium of human preimplantation embryo through deep learning

   Zhenyi Zhang^†, Jie Qiao, Yidong Chen^*, and Peijie Zhou^*

   Advanced Science (Q1, IF: 14.1) , Jun 2025

   Abs DOI HTML

   Noninvasive preimplantation genetic testing for aneuploidy based on embryonic cell-free DNA (cfDNA) released in spent embryo culture media (SECM) has brought hope in selecting embryos that are most likely to implant and grow into healthy babies during assisted reproduction. However, maternal DNA contamination in SECM significantly hampers the reliability of embryonic chromosome ploidy profiles, leading to false negative results, particularly at high contamination levels. Here, we present DECENT (deep copy number variation (CNV) reconstruction), a deep learning method to reconstruct embryonic CNVs and mitigate maternal contamination in SECM from single-cell methylation sequencing of cfDNA. DECENT integrates sequence features and methylation patterns by combining convolution modules, long-short memory, and attention mechanisms to infer the origin of cfDNA reads. The benchmarking study demonstrated DECENT’s ability to estimate contamination proportions and restore embryonic chromosome aneuploidies in samples with varying contamination levels. In contaminated SECM clinical samples, including one with more than 80% maternal reads, DECENT achieved consistent CNV recovery with invasive tests. Overall, DECENT contributes to enhancing the diagnostic accuracy and effectiveness of cfDNA-based noninvasive preimplantation genetic testing, establishing a robust groundwork for its extensive clinical utilization in the field of reproductive medicine.

5. CiCP

   

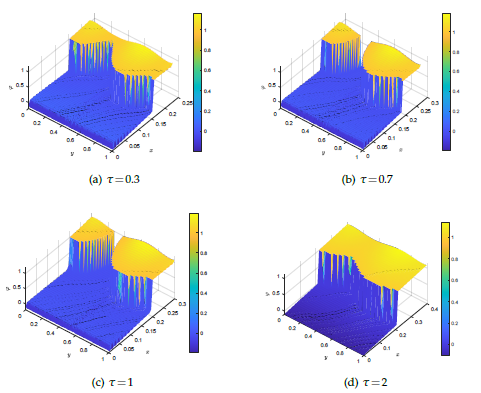   Uncertainty Quantification of Phase Transition Problems with an Injection Boundary

   Zhenyi Zhang^†, Shengbo Ma, and Zhennan Zhou^*

   Communications in Computational Physics, Nov 2025

   Abs DOI HTML

   We develop an enthalpy-based modeling and computational framework to quantify uncertainty in Stefan problems with an injection boundary. Inspired by airfoil icing studies, we consider a system featuring an injection boundary inducing domain changes and a free boundary separating phases, resulting in two types of moving boundaries. Our proposed enthalpy-based formulation seamlessly integrates thermal diffusion across the domain with energy fluxes at the boundaries, addressing a modified injection condition for boundary movement. Uncertainty then stems from random variations in the injection boundary. The primary focus of our Uncertainty Quantification (UQ) centers on investigating the effects of uncertainty on free boundary propagation. Through mapping to a reference domain, we derive an enthalpy-based numerical scheme tailored to the transformed coordinate system, facilitating a simple and efficient simulation. Numerical and UQ studies in one and two dimensions validate the proposed model and the extended enthalpy method. They offer intriguing insights into ice accretion and other multiphysics processes involving phase transitions.

6. Entropy

   

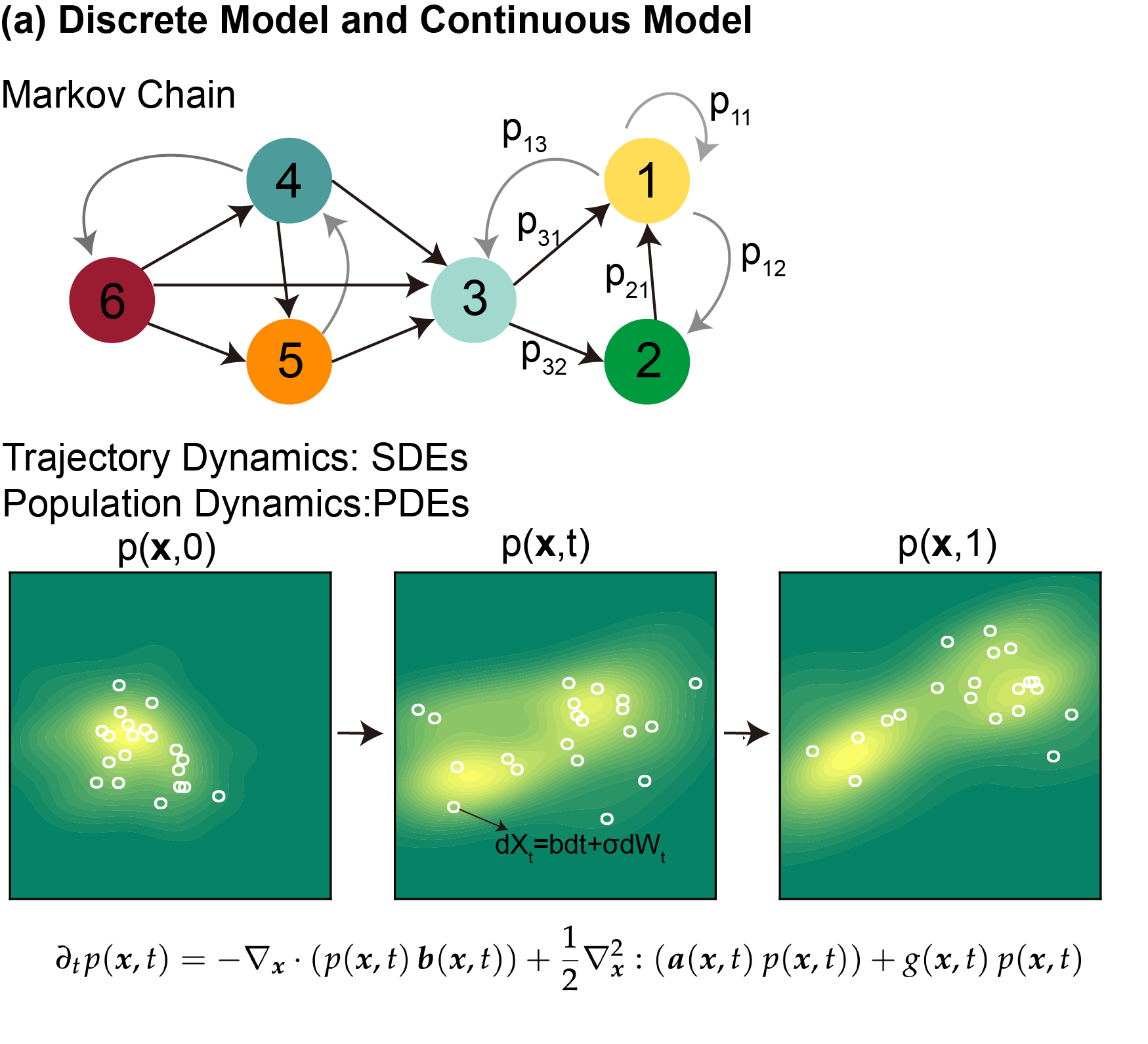   Integrating Dynamical Systems Modeling with Spatiotemporal scRNA-Seq Data Analysis

   Zhenyi Zhang^†, Yuhao Sun^†, Qiangwei Peng^†, Tiejun Li^*, and Peijie Zhou^*

   Entropy, Nov 2025

   Abs DOI HTML

   Understanding the dynamic nature of biological systems is fundamental to deciphering cellular behavior, developmental processes, and disease progression. Single-cell RNA sequencing (scRNA-seq) has provided static snapshots of gene expression, offering valuable insights into cellular states at a single time point. Recent advancements in temporally resolved scRNA-seq, spatial transcriptomics (ST), and time-series spatial transcriptomics (temporal-ST) have further revolutionized our ability to study the spatiotemporal dynamics of individual cells. These technologies, when combined with computational frameworks such as Markov chains, stochastic differential equations (SDEs), and generative models like optimal transport and Schrödinger bridges, enable the reconstruction of dynamic cellular trajectories and cell fate decisions. This review discusses how these dynamical system approaches offer new opportunities to model and infer cellular dynamics from a systematic perspective.

7. AAAI 2026 oral

   

   CellStream: Dynamical Optimal Transport Informed Embeddings for Reconstructing Cellular Trajectories from Snapshots Data

   Yue Ling^†, Peiqi Zhang^†, Zhenyi Zhang^*, and Peijie Zhou^*

   AAAI 2026 oral, Nov 2025

   Abs DOI HTML

   Single-cell RNA sequencing (scRNA-seq), especially temporally resolved datasets, enables genome-wide profiling of gene expression dynamics at single-cell resolution across discrete time points. However, current technologies provide only sparse, static snapshots of cell states and are inherently influenced by technical noise, complicating the inference and representation of continuous transcriptional dynamics. Although embedding methods can reduce dimensionality and mitigate technical noise, the majority of existing approaches typically treat trajectory inference separately from embedding construction, often neglecting temporal structure. To address this challenge, here we introduce CellStream, a novel deep learning framework that jointly learns embedding and cellular dynamics from single-cell snapshot data by integrating an autoencoder with unbalanced dynamical optimal transport. Compared to existing methods, CellStream generates dynamics-informed embeddings that robustly capture temporal developmental processes while maintaining high consistency with the underlying data manifold. We demonstrate CellStream’s effectiveness on both simulated datasets and real scRNA-seq data, including spatial transcriptomics. Our experiments indicate significant quantitative improvements over state-of-the-art methods in representing cellular trajectories with enhanced temporal coherence and reduced noise sensitivity. Overall, CellStream provides a new tool for learning and representing continuous streams from the noisy, static snapshots of single-cell gene expression.

8. NeurIPS 2025

   

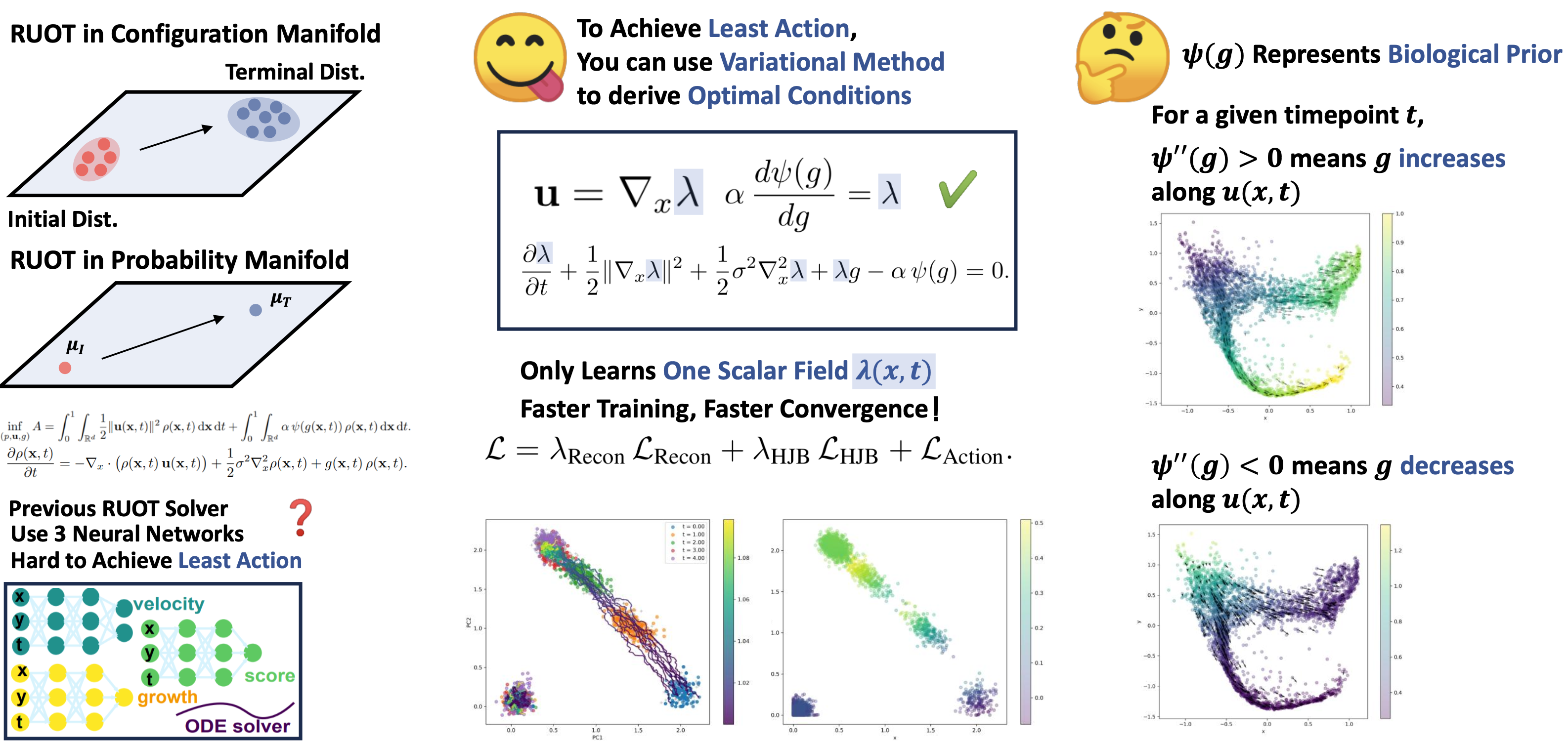   Variational Regularized Unbalanced Optimal Transport: Single Network, Least Action

   Yuhao Sun^†, Zhenyi Zhang^†, Zihan Wang^†, Tiejun Li^*, and Peijie Zhou^*

   Advances in Neural Information Processing Systems  (NeurIPS) , May 2025

   Abs DOI HTML

   Recovering the dynamics from a few snapshots of a high-dimensional system is a challenging task in statistical physics and machine learning, with important applications in computational biology. Many algorithms have been developed to tackle this problem, based on frameworks such as optimal transport and the Schrödinger bridge. A notable recent framework is Regularized Unbalanced Optimal Transport (RUOT), which integrates both stochastic dynamics and unnormalized distributions. However, since many existing methods do not explicitly enforce optimality conditions, their solutions often struggle to satisfy the principle of least action and meet challenges to converge in a stable and reliable way. To address these issues, we propose Variational RUOT (Var-RUOT), a new framework to solve the RUOT problem. By incorporating the optimal necessary conditions for the RUOT problem into both the parameterization of the search space and the loss function design, Var-RUOT only needs to learn a scalar field to solve the RUOT problem and can search for solutions with lower action. We also examined the challenge of selecting a growth penalty function in the widely used Wasserstein-Fisher-Rao metric and proposed a solution that better aligns with biological priors in Var-RUOT. We validated the effectiveness of Var-RUOT on both simulated data and real single-cell datasets. Compared with existing algorithms, Var-RUOT can find solutions with lower action while exhibiting faster convergence and improved training stability.

9. NeurIPS 2025

   

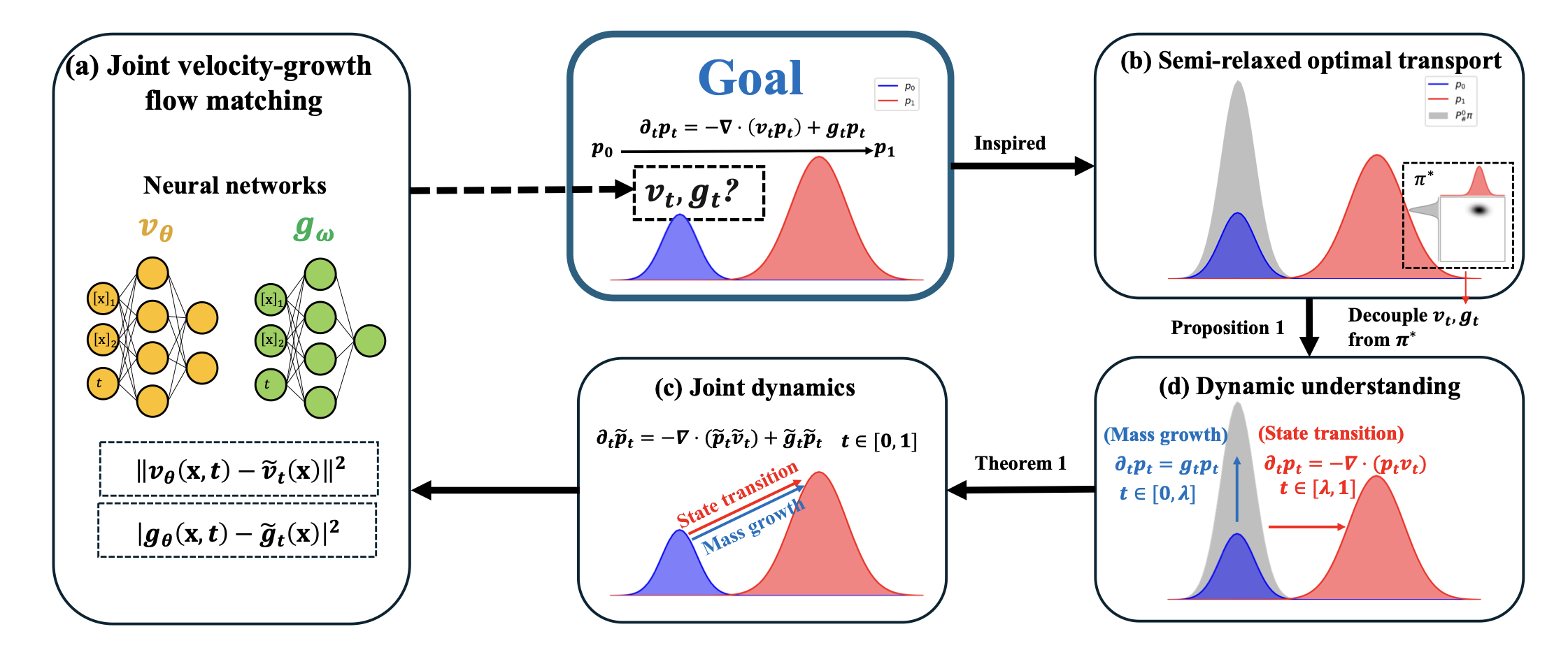   Joint Velocity-Growth Flow Matching for Single-Cell Dynamics Modeling

   Dongyi Wang^†, Yuanwei Jiang^†, Zhenyi Zhang^†, Xiang Gu^*, Peijie Zhou^*, and Jian Sun^*

   Advances in Neural Information Processing Systems  (NeurIPS) , May 2025

   Abs DOI HTML

   Learning the underlying dynamics of single cells from snapshot data has gained increasing attention in scientific and machine learning research. The destructive measurement technique and cell proliferation/death result in unpaired and unbalanced data between snapshots, making the learning of the underlying dynamics challenging. In this paper, we propose joint Velocity-Growth Flow Matching (VGFM), a novel paradigm that jointly learns state transition and mass growth of single-cell populations via flow matching. VGFM builds an ideal single-cell dynamics containing velocity of state and growth of mass, driven by a presented two-period dynamic understanding of the static semi-relaxed optimal transport, a mathematical tool that seeks the coupling between unpaired and unbalanced data. To enable practical usage, we approximate the ideal dynamics using neural networks, forming our joint velocity and growth matching framework. A distribution fitting loss is also employed in VGFM to further improve the fitting performance for snapshot data. Extensive experimental results on both synthetic and real datasets demonstrate that VGFM can capture the underlying biological dynamics accounting for mass and state variations over time, outperforming existing approaches for single-cell dynamics modeling.